Ⅰ. Schematic Diagram of Coordinate Transform
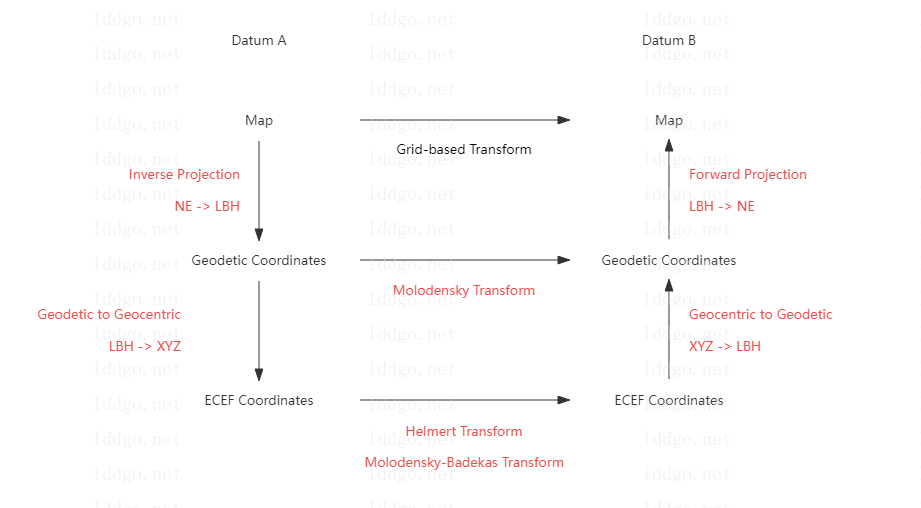
Ⅱ. List of Coordinate Conversion Tools
| Category | Tool | Description | Note |
|---|---|---|---|
| Map <-> Map | Map Coordinate System Converter Online | Coordinate Conversion between Different Plane Map Coordinate Systems | Supports GCJ02, BD09, and WGS84 coordinates |
| Geodetic <-> Geodetic | Molodensky Transform Online | Coordinate transformation between different geodetic coordinate system | Support customization of multiple geodetic coordinate system through ellipsoids |
| Geocentric <-> Geocentric | Coordinate Frame Convert Online | Coordinate conversion between different earth centered earth fixed coordinate system (spatial Cartesian coordinate system) | Supports coordinate conversion with three, four, and seven parameters. Including Bolsa-Wolf coordinate transformation |
| Molodensky-Badekas Transform Online | Coordinate conversion between different earth centered earth fixed coordinate system (spatial Cartesian coordinate system) | Ten parameter coordinate conversion | |
| Map <-> Geodetic | Coordinate Projection Calculator Online | Projections map the spherical 3D space to a flat 2D space | Supports multiple projection algorithms such as Mercator, web Mercator, and Unified Transverse Mercator (UTM) |
| Geodetic <-> Geocentric | Geodetic to Cartesian Coordinates Converter Online | Conversion between geodetic coordinates and earth centered earth fixed coordinates | Support for custom ellipsoids |
| Topocentric <-> Geocentric | Geocentric to Topocentric Converter Online | Conversion between station center coordinates and earth centered earth fixed coordinates | Support multiple ways to define the origin of the Topocentric center |
| Plane <-> Polar | Cartesian and Polar Coordinate Converter Online | Conversion between Cartesian and Polar Coordinates | |
| Geodetic Latitude <-> Geocentric Latitude | Geodetic Latitude to Geocentric Latitude Converter Online | Conversion between geodetic latitude and geocentric latitude | Support custom ellipsoid |
| Axis Swap | Axis Swap Online | Exchange the order and sign of X, Y, and Z values for a set of coordinates | |
| Unit Convert | Coordinate Unit Converter Online | Convert the units of various fields in coordinates, supporting the conversion of length units, angle units, and time units in coordinates |
Ⅲ. Introduction to Coordinate Systems
- Geodetic Coordinate System : A geodetic datum or geodetic system (also: geodetic reference datum, geodetic reference system, or geodetic reference frame) is a global datum reference or reference frame for precisely representing the position of locations on Earth or other planetary bodies by means of geodetic coordinates. Datums are crucial to any technology or technique based on spatial location, including geodesy, navigation, surveying, geographic information systems, remote sensing, and cartography. A horizontal datum is used to measure a location across the Earth's surface, in latitude and longitude or another coordinate system; a vertical datum is used to measure the elevation or depth relative to a standard origin, such as mean sea level (MSL). Since the rise of the global positioning system (GPS), the ellipsoid and datum WGS 84 it uses has supplanted most others in many applications. The WGS 84 is intended for global use, unlike most earlier datums.
- Earth-centered, Earth-fixed Coordinate System : The Earth-centered, Earth-fixed coordinate system (acronym ECEF), also known as the geocentric coordinate system, is a cartesian spatial reference system that represents locations in the vicinity of the Earth (including its surface, interior, atmosphere, and surrounding outer space) as X, Y, and Z measurements from its center of mass.Its most common use is in tracking the orbits of satellites and in satellite navigation systems for measuring locations on the surface of the Earth, but it is also used in applications such as tracking crustal motion.
- Polar Coordinate System : In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a reference point and an angle from a reference direction. The reference point (analogous to the origin of a Cartesian coordinate system) is called the pole, and the ray from the pole in the reference direction is the polar axis. The distance from the pole is called the radial coordinate, radial distance or simply radius, and the angle is called the angular coordinate, polar angle, or azimuth. Angles in polar notation are generally expressed in either degrees or radians (2π rad being equal to 360°). Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more intuitive to model using polar coordinates.
The coordinate system conversion instruction document introduces various coordinate systems and the applicability of various coordinate conversion tools on this website.
